Pythonのコードで、CSVやExcelのデータを読み込んだり、統計指標を使ったりする機会は、普段Pythonを使っている方であれば使い慣れている方もいらっしゃると思いますが、実際には少し興味はあるけれど、どうPythonで書いてみればよいのかわからないという方のほうが多いのではないでしょうか。ここではPythonのライブラリの基本的な書き方を含め、読み込んだCSVデータの内容を、統計的に処理・表現するという形の演習をしていきたいと思います。
「数学的な問題をPythonで簡単なスクリプトを作って動作を確認する」こと通して、Pythonに触れる機会をつくっていきたいと考えています。Pythonに慣れるという点でも手を動かして考える機会にして頂ければ幸いです。
今回は、Pythonで学び直す数学【統計編】の確認をしていきたいと思います。
演習問題のダウンロードはこちらから
Contents
Pythonライブラリ~Numpy, Pandasとは?
まず、読み込んだデータを統計情報として利用するためのPythonライブラリについてみていきましょう。
ここでは「Numpy」と「Pandas」を紹介します。
Numpyとは?
Numpyとは、科学計算のための基本的なパッケージで、アレイを作成するのに便利なライブラリのこと。
Numpyを利用するには、以下のようにインポートを行います。Asキーワードを使用してnpで呼び出せるようにします。
In
import numpy as np
▷使用例
# 1次元配列の作成 a = np.array( [1, 2, 3] ) # 2次元配列の作成 b = np.array([ [1, 2, 3], [4, 5, 6] ]) # 等差数列の配列を返す(arange) np.arange( 1, 11 ) Out >>> array( [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] ) np.arange( 1, 11, 2) Out >>> array( [1, 3, 5, 7, 9] )
NumPyを使用することで、アレイや乱数生成など様々なことができるようになります。通常のPythonで処理を行うよりもずっと早く処理できるので、大量のデータを扱う(機械学習など)場合にNumPyが利用されます。
Pandasとは?
Pandasとは、Pythonでデータ処理をするために作られた高機能なライブラリのこと。代表的な使い方としてSeriesやDataFrameを使ったデータの処理方法があります。
Pandasを利用するには、以下のようにインポートを行います。Asキーワードを使用してpdで呼び出せるようにします。
In
import pandas as pd
▷使用例
# 1次元データの利用
ser = pd.Series( [10, 20, 30, 40] )
# 2次元データの利用
df = pd.DataFrame( [10, “a”, True],
[20, “b”, False],
[30, “c”, False],
[40, “d”, True] )
df
csvやExcelのデータを読み込んだり、列や行を削除したり、フィルターをかけて抽出をしたり、Excelやデータベース言語のSQLでできることがPandasの機能にあります。
CSVファイルの読み込み
次に、統計として扱うCSVデータを読み込む方法について、見ていきましょう。
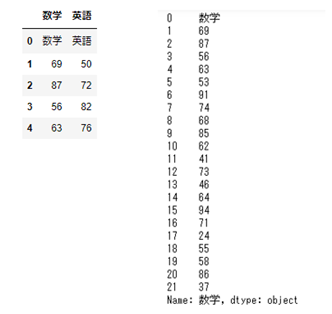
以下のようなCSVデータを読み込む例を考えてみましょう。

In
import pandas as pd
# testScore.csv の読み込み
col_names = ['数学','英語']
data = pd.read_csv('testScore.csv', names = col_names, encoding='SHIFT-JIS')
# 5件分の内容を確認
data.head()
# 数学の全データを参照
data['数学']
Out
度数分布表を描画
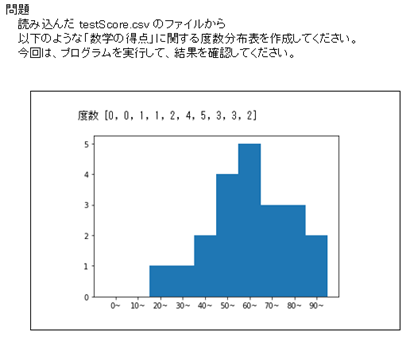
次に、度数分布表を描画する方法について、見ていきましょう。
In
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
# testScore.csv の読み込み
nameColumns = ['数学', '英語']
testData = pd.read_csv('testScore.csv', header = None, skiprows=1, names = nameColumns, encoding='SHIFT-JIS')
# 各階層に含まれる度数を数える
hist = [0]*10
for data in testData['数学']:
if int(data) < 10: hist[0] += 1
elif int(data) < 20: hist[1] += 1
elif int(data) < 30: hist[2] += 1
elif int(data) < 40: hist[3] += 1
elif int(data) < 50: hist[4] += 1
elif int(data) < 60: hist[5] += 1
elif int(data) < 70: hist[6] += 1
elif int(data) < 80: hist[7] += 1
elif int(data) < 90: hist[8] += 1
elif int(data) <= 100: hist[9] += 1
print('度数', hist)
# 度数分布図
x = list(range(1, 11)) # x軸の値
labels = ['0~', '10~', '20~', '30~', '40~', '50~', '60~', '70~', '80~', '90~']
# x軸の目盛りラベル
plt.bar(x, hist, tick_label=labels, width=1) # 棒グラフを描画
plt.show()
統計指標(平均値,中央値,最頻値)
ここで、添付演習問題の「統計指標」シートの問題を解いてみましょう。
Numpyを使った平均値と中央値の求め方を調べて、下線部に入る式を埋めてみましょう。

分散と標準偏差
ここで、添付演習問題の「分散と標準偏差」シートの問題を解いてみましょう。
Numpyを使った分散と標準偏差の求め方を調べて、下線部に入る式を埋めてみましょう。

偏差値を算出
ここで、添付演習問題の「偏差値算出」シートの問題を解いてみましょう。

====================================
以前学校で学んできた内容をもとにPythonでスクリプトを実行しながら確認できるのは面白いなと感じる方もいらっしゃるかもしれません。自分にできる範囲のものから少しずつPythonにも挑戦してみようかなと思っていただければ幸いです。
以上となります。
#edu-IT #名古屋
参考文献:
・谷尻かおり『文系プログラマーのためのPythonで学び直す高校数学』日経BP社(2021年)





