仕事や趣味でPythonのコードを書いている方であれば、「JupyterNotebookを使ってグラフを描画」といってピンとくる方も多いと思いますが、実際に興味はあるけれど、どう使ってみればよいのかわからないという方も多いと思います。Pythonのライブラリの基本的な書き方を含め、学生時代に習った数学の問題を通して、グラフを描画するという形で演習をしていきたいと思います。
「数学的な問題をPythonで簡単なスクリプトを作って動作を確認する」こと通して、Pythonに触れる機会をつくっていきたいと考えています。Pythonに慣れるという点でも手を動かして考える機会にして頂ければ幸いです。
今回は、Pythonで学び直す数学【関数とグラフ・微分積分編】の確認をしていきたいと思います。
演習問題のダウンロードはこちらから
グラフ描画~matplotlibの使い方
数学の授業で、程式を習った際に、方眼紙を用いて作図をした、という方もいらっしゃるかもしれません。Pythonでは「matplotlib」というライブラリでグラフや図形を描画することができます。
実際に、今回のテーマである「関数とグラフ/微分積分」について、以下の例題のPythonのコードを考えていきます。
・直交する直線
・連立方程式/2直線の交点
・関数と導関数
・接線
・定積分の計算
それでは、「Maplotlibでグラフを描画」する方法からみていきましょう。
Matplotlibとは
Matplotlibとは、Pythonで主に2次元のグラフを描画するためのライブラリのこと。
Matplotlibを利用するには、以下のようにインポートを行います。Asキーワードを使用してpltで呼び出せるようにします。
In
import matplotlib.pyplot as plt
まずは折れ線グラフの書き方から
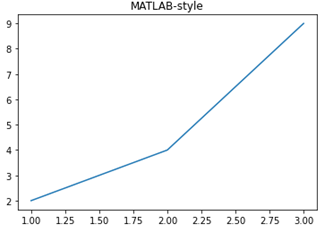
上図の折れ線グラフは以下のコードを記述することで表現できます。
In
# データを用意
x = [1,2,3]
y = [2,4,9]
plt.plot(x,y) # 折れ線グラフを描画
plt.title('MATLAB-style') # グラフにタイトルを設定
plt.show() # グラフを表示
x座標とy座標を与えてplot関数に引数として渡すことで、棒グラフを描画することができるのですね。
(x, y)が1つあれば点を描画でき、もう1つ(x2, y2) あれば、2点を結ぶ直線ができ、
細かく座標を取っていけば、関数のグラフも描画できる、といった具合に応用して考えることができます。
一次方程式
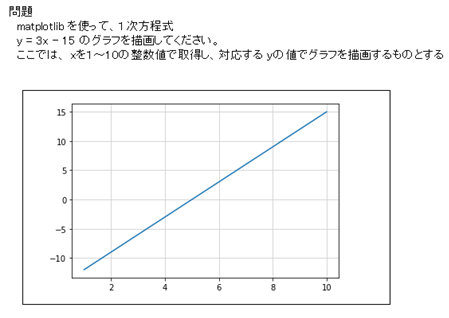
以下のような一次方程式のグラフを描画する例を考えてみましょう。
Xを1~10の整数値で取得する方法として、range関数を利用することで開始値から終了までの連続した値を要素を生成します。
>>> range(5) # range(stop) 0 1 2 3 4 >>> range(1,11) # range(start, stop) 1 2 3 4 5 6 7 8 9 10 >>> range(1,11, 2) # range(start, stop, step) 1 3 5 7 9
y = 3x – 15 のグラフ を描くには、上のようにxの値(リスト)を取得し、それに対応するyの値(リスト)をplot関数に引数として渡します。
%matplotlib inline
import matplotlib.pyplot as plt
# データ
x = list(range(1, 11)) # x の値(1~10)
y = []
for i in range(10):
y.append(3*x[i] - 15) # y= 3x-15
# グラフ
plt.plot(x, y)
plt.grid(color='0.8')
plt.show()
また、配列や行列を効率よく扱うことができるパッケージである「numpy」 をインポートしてから利用することで、より簡易的に直線の方程式を「yにxを代入する式」として記述することができます。
xを1~10の整数値で取得する方法として、arange関数を利用することで開始値から終了までの連続した値を要素を生成します。
>>>import numpy as np >>> np.arange(5) # arange(stop) 0 1 2 3 4 >>> np.arange(1,11) # arange(start, stop) 1 2 3 4 5 6 7 8 9 10 >>> np.arange(1,11, 2) # arange(start, stop, step) 1 3 5 7 9
%matplotlib inline import matplotlib.pyplot as plt import numpy as np # データ x = np.arange(1, 11) # x の値(1~10) y = 3*x + 15 # グラフ plt.plot(x, y) plt.grid(color='0.8') plt.show()
⇒ ここで類題として、添付資料「直交する直線」シートにある演習問題を解いてみましょう
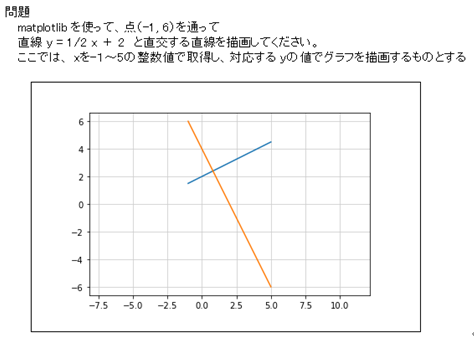
連立方程式
Pythonのライブラリを使った連立方程式の解き方をみていきましょう。
具体的には、SymPyの中からSymbolクラスのオブジェクトを生成して、solve関数を実行して求めます。
例をみていきましょう。

from sympy import Symbol, solve
# 式を定義
a = Symbol('a') -①
b = Symbol('b') -②
ex1 = a + b - 3
ex2 = 5*a + 2*b -12
# 連立方程式を解く
print(solve((ex1, ex2)))
⇒ ここで類題として、添付資料「2直線の交点」シートにある演習問題を解いてみましょう

matplotlibを使って、関数とグラフを描画する方法とPythonのライブラリを利用して直線の交点を求める方法について紹介しました。
これまでの知識をもとに、方程式のグラフを描画する以下の演習を解いてみましょう。
関数と導関数
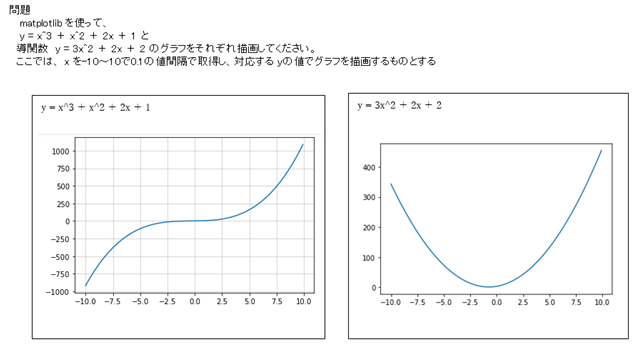
接線を描画
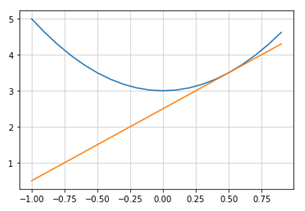
定積分

====================================
以前学校で学んできた内容をもとにPythonでスクリプトを実行しながら確認できるのは面白いなと感じる方もいらっしゃるかもしれません。自分にできる範囲のものから少しずつPythonにも挑戦してみようかなと思っていただければ幸いです。
以上となります。
#edu-IT #名古屋
参考文献:
・谷尻かおり『文系プログラマーのためのPythonで学び直す高校数学』日経BP社(2021年)





